2) Parcours de graphes
Listes d'adjacence - liste d'adjacence
Ce nom est trompeur, mais très souvent utilisé.
On appelle souvent "listes d'adjacence", ou même "liste d'adjacence", le dictionnaire dont les clés
sont les sommets du graphes, et les valeurs les listes (parfois tuples) des voisins associés à chaque sommet.
I. Introduction : modéliser un labyrinthe⚓︎
Considérons les problèmes suivants :
- Comment rechercher le chemin le plus court entre deux stations dans le métro? Indépendamment de l'aspect ludique, c'est en fait un problème difficile qu'on aurait bien du mal à résoudre de façon raisonnable sur un gros graphe comme celui du métro.
- Comment trouver la sortie d'un labyrinthe?
Les labyrinthes⚓︎
Voici l'image d'un labyrinthe :
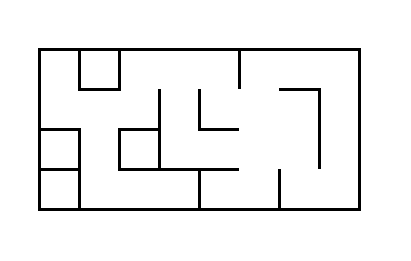
Ce labyrinthe peut être représenté par le graphe suivant :
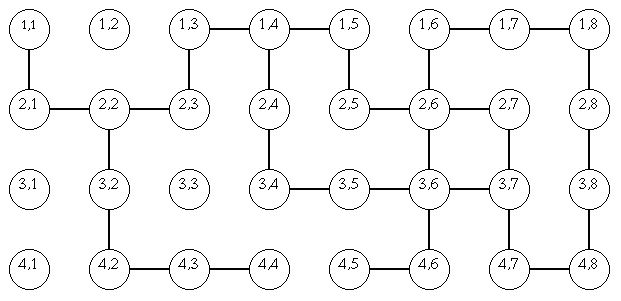
-
Chaque sommet du graphe correspond à une case du labyrinthe
-
une arête relie 2 cases voisines quand le passage est possible.
-
Si une paroie empêche de passer on ne met pas l'arête.
Par exemple il n'y a pas d'arête entre les sommets (1,1) et (1,2) mais il y en a une entre (1,1) et (2,1).
Les noeuds
A quoi correspondent les deux chiffres des noeuds de cette représentation ?
Solution
Le premier chiffre est un numéro de ligne, le deuxième un numéro de colonne.
Nous allons représenter ce graphe par le dictionnaire suivant :
graphe = {11: [21], 12: [], 13: [23, 14], 14: [13, 15, 24], 15: [14, 25], 16: [26, 17], 17: [16, 18], 18: [17, 28],
21: [11, 22], 22: [21, 23, 32], 23: [22, 13], 24: [14, 34], 25: [15, 26], 26: [25, 16, 36, 27],
27: [37, 26], 28: [18, 38], 31: [], 32: [22, 42], 33: [], 34: [24, 35], 35: [34, 36],
36: [26, 35, 46, 37], 37: [27, 36, 47], 38: [28, 48], 41: [], 42: [32, 43], 43: [42, 44], 44: [43],
45: [46], 46: [36, 45], 47: [37, 48], 48: [47, 38]}
Dessiner ce graphe avec netwoks
Dessiner ce graphe avec graphviz
Créer un fichier png de ce graphe avec graphviz
Résoudre ce labyrinthe
Ce labyrinthe est assez simple, et une fois sa représentation en graphe tracée comme ci-dessus, il semble assez facile de résoudre ce labyrinthe, c'est à dire de trouver un chemin qui permette d'aller d'une case "entrée" à une case "sortie".
Supposons que la case "entrée" soit la case (1,1) et la case sortie la case (4,8). Cela correspond respectivement aux noeuds 11 et 48. Observons le graphe précédent. On voit assez facilement plusieurs chemins possibles. En donner trois possibles.
Solution
- 11-21-22-23-13-14-15-25-26-16-17-18-28-38-48
- 11-21-22-23-13-14-24-34-35-36-37-47-48
- 11-21-22-23-13-14-24-34-35-36-26-16-17-18-28-38-48
Quels parcours ?
Nous voulons écrire un script Python qui permette de résoudre automatiquement, dans le cas où c'est possible, n'importe quel labyrinthe, même très compliqué.
Pour cela on peut penser parcourir le graphe en partant de l'entrée, en suivant différents chemins, jusqu'à atteindre le sommet de sortie.
Plusieurs algorithmes "classiques" permettent de parcourir les graphes. Nous allons commencer par les étudier, puis nous essaierons de résoudre ce problème en choisissant l'algorithme le plus adapté à cette situation.
II. Les parcours de graphes⚓︎
Contrairement aux arbres, les graphes n’ont pas de racine, de « début ». On peut donc choisir n’importe quel sommet pour commencer le parcours. Ceci dit, le parcours de certains graphes orientés demande un choix de sommet de début réfléchi.
😅 La vidéo suivante explique le principe des parcours. Pour bien justifier l'utilisation de la pile, la première étape du premier parcours présenté n'est pas tout à fait celle du parcours en profondeur que nous verrons au IV.
A retenir
- Parcours en largeur : File
- Pacours en profondeur : Pile
III. Le parcours en largeur⚓︎
Parcours en largeur
parcours est la liste vide qui contiendra les sommets visités par parcours en largeur
F est une file vide
On enfile un sommet dans F
Tant que F n'est pas vide
S = Tête de F
On défile F et on ajoute le sommet dans parcours
On enfile les voisins de S qui ne sont ni dans la file ni dans parcours
Fin Tant Que
👉 9 étapes :









Question
Ecrire le code d'une fonction parcours_en_largeur qui parcourt en largeur un graphe à partir du sommet depart et dont
sa liste d'adjacence est representée par un dictionnaire nommé graphe.
Cette fonction renverra la liste des sommets parcourus en partant du sommet depart.
Compléter le script ci-dessous :
Graphe du test :

Optimisation
Le coût d'une recherche dans une liste (pour tester si un sommet a déjà été visité) est beaucoup plus important que le coût de la recherche dans un ensemble (hors programme NSI), ou dans un dictionnaire. ( Les tables de hash)
Nous allons donc proposer une autre version pour améliorer l'efficacité de l'algorithme.
- Un sommet est "parcouru" lorsqu'il a été mis dans la liste
parcours - Un sommet est "en attente" lorqu'il est dans la file.
- Tous les autres sommets sont "pas vu".
Compléter le script suivant :
# Tests (insensible à la casse)(Ctrl+I)
(Alt+: ; Ctrl pour inverser les colonnes)
(Esc)
Distances croissantes
On peut remarquer que l'algorithme de parcours en largeur permet de dresser la liste des sommets d'un graphe par distance croissante au sommet d'origine

A partir du sommet A représenté en bleu,on a par distance croissante :
- Les sommets à une distance de 1 du sommet A représentés en vert : B, D, E
- Les sommets à une distance de 2 du sommet A représentés en rouge : C, F, G
- Le sommet à une distance de 3 du sommet A représenté en jaune : H
On retrouve bien dans la liste renvoyée par la fonction de parcours en largeur à partir du sommet A les sommets classés par ordre de distance croissante au sommet A : ['A', 'B', 'D', 'E', 'C', 'F', 'G', 'H'].
Note
💡 On peut se servir du parcours en largeur pour trouver un chemin de distance minimale entre deux sommets.
IV. Le parcours en profondeur⚓︎
1. Le parcours en profondeur récursif⚓︎
Une première approche⚓︎
Parcours en profondeur
Parcours en profondeur ou DFS en anglais pour Depth First Search
Le parcours en profondeur est un parcours où on va aller «le plus loin possible» sans se préoccuper dans un premier temps des autres voisins non visités :
On va visiter le premier des voisins du sommet non traités, puis faire de même avec lui (visiter le premier de ses voisins non traités), etc. Lorsqu'il n'y a plus de voisin, on revient en arrière pour aller voir le dernier voisin non visité.
Dans un labyrinthe, ce parcours s'explique très bien : on prend par exemple tous les chemins sur la droite jusqu'à rencontrer un mur, auquel cas on revient au dernier embranchement et on prend un autre chemin, puis on repart à droite, etc. Attention, pour ne pas tourner en rond autour d'un bloc, il faut marquer les endroits par lesquels on est déjà passés.
C'est un parcours qui s'écrit naturellement de manière récursive.
Méthode récursive
L’ensemble des sommets déjà visités est stocké dans un objet Python (liste, ou dictionnaire, ou ensemble).
La visite est relancée récursivement pour chaque voisin du sommet visité qui n'a pas déjà été visité.
A vous
Compléter le code de la fonction parcours_profondeur qui parcourt en profondeur un graphe à partir du sommet sommet
et dont sa liste d'adjacence est representée par un dictionnaire nommé graphe.
Cette fonction renverra la liste des sommets parcourus en partant du sommet depart.
🌵 Il peut falloir plusieurs lignes de code pour remplacer les ...
Graphe du test :

# Tests (insensible à la casse)(Ctrl+I)
(Alt+: ; Ctrl pour inverser les colonnes)
(Esc)
return ou pas return ?
Testons sur le graphe suivant :
Dans les deux cas suivants la différence se situe ligne 7.Sans return pour l'appel récursif de la fonction
Avec return pour l'appel récursif de la fonction
Que s'est-il passé ?
Solution
Le return devant l'appel récursif empêche de remonter au sommet A, pour explorer la branche suivante.
On est coincé dans un cul de sac.
Optimisation⚓︎
Optimisation
Le coût d'une recherche dans une liste (pour tester si un sommet a déjà été visité) est beaucoup plus important que le coût de la recherche dans un ensemble (hors programme NSI), ou dans un dictionnaire.
Nous allons donc proposer une autre version pour améliorer l'efficacité de l'algorithme.
A vous
Compléter le script.
Graphe du test :

# Tests (insensible à la casse)(Ctrl+I)
(Alt+: ; Ctrl pour inverser les colonnes)
(Esc)
Autre possibilité
On peut aussi construire le parcours par concaténation de listes.
Tester ci-dessous :
# Tests (insensible à la casse)(Ctrl+I)
(Alt+: ; Ctrl pour inverser les colonnes)
(Esc)
2. Le parcours en profondeur itératif⚓︎
Une première approche⚓︎
Algorithme itératif avec une pile
Comme nous l'avons vu dans la vidéo, on peut aussi utiliser une pile.
✍ A noter ... et à mémoriser ... 🐘
parcours est la liste vide qui contiendra les sommets visités par parcours en profondeur
P est une pile vide
On empile un sommet dans P
Tant que P n'est pas vide
S = dépile(P)
On ajoute S à parcours
On empile les voisins de S qui ne sont ni dans la pile ni dans parcours
Fin Tant Que
👉 9 étapes :









A vous
Ecrire le code d'une fonction parcours_en_profondeur qui parcourt en profondeur un graphe à partir du sommet depart
et dont sa liste d'adjacence est representée par un dictionnaire nommé graphe
Cette fonction renverra la liste des sommets parcourus en partant du sommet depart.
Compléter le script ci-dessous de façon itérative :
Graphe du test :

# Tests (insensible à la casse)(Ctrl+I)
(Alt+: ; Ctrl pour inverser les colonnes)
(Esc)
Différents parcours en profondeur ?⚓︎
Il y a souvent plusieurs possibilités
Observez les résultats obtenus pour le parcours en profondeur par algorithme récursif, ou itératif.
🌵 Les parcours obtenus sont différents. De plus, suivant l'ordre des listes d'adjacences, on obtiendra aussi des résultats de parcours différents.
🎲 Dans la vidéo d'introduction, on était amené à faire des choix arbitraires.
Optimisation⚓︎
Optimisation
Le coût d'une recherche dans une liste (pour tester si un sommet a déjà été visité) est beaucoup plus important que le coût de la recherche dans un ensemble (hors programme NSI), ou dans un dictionnaire.
Nous allons donc proposer une autre version pour améliorer l'efficacité de l'algorithme.
A vous
- Un sommet est "parcouru" lorsqu'il a été mis dans la liste
parcours - Un sommet est "en attente" lorqu'il est dans la pile.
- Tous les autres sommets sont "pas vu".
Graphe du test :

# Tests (insensible à la casse)(Ctrl+I)
(Alt+: ; Ctrl pour inverser les colonnes)
(Esc)
V. Bilan⚓︎
A retenir
-
Dans le parcours en largeur, on visite tous les sommets en «cercle concentriques» autour du sommet de départ : d’abord les voisins directs, puis les voisins des voisins directs etc, et on continue jusqu’à ce qu’il n’y ait plus de sommets à visiter.
👉 On utilise une file. -
Le parcours en profondeur d’un graphe à partir d’un sommet consiste à suivre les arêtes arbitrairement, en marquant les sommets déjà visités pour ne pas les visiter à nouveau. On avance le plus possible et on recule quand on est bloqué.
👉 On utilise un algorithme récursif, ou une pile.
VI. Le labyrinthe⚓︎
TP : résolution d'un labyrinthe
Après avoir téléchargé le fichier, vous pourrez le lire à partir de Basthon
🌐 TD à télécharger : Fichier TP_resolution_labyrinthe_sujet.ipynb : "Clic droit", puis "Enregistrer la cible du lien sous"
😊 La correction est arrivée :
🌐 Fichier TP_resolution_labyrinthe_corr.ipynb : "Clic droit", puis "Enregistrer la cible du lien sous"
VII. Remarque⚓︎
Retour sur l'efficacité
🌵 ma_liste.pop(0)
Pour une question de simplification des codes, Nous avons souvent utilisé ma_liste.pop(0)
Ce n'est pas une façon efficace de procéder, car le temps d'exécution est proportionnel à la taille de la liste ma_liste
Recopier dans votre éditeur Python (pas sur Basthon) le script suivant, puis l'exécuter :
import timeit
import matplotlib.pyplot as plt
def suppression_debut(lst):
lst.pop(0)
# différentes tailles de listes notées n dans la suite
abscisse = [(10**7)*i for i in range(1, 11)]
print(abscisse)
ordonnee = []
for n in abscisse:
temps = 0
for i in range(2):
ma_liste = [0]*n # Création de liste de tailles n
# Le chronométrage étant fait 2 fois, Il faut donc pour chaque mesure reprendre la liste initiale
temps += timeit.timeit("suppression_debut(ma_liste)", number=1, globals=globals())
ordonnee.append(temps)
# Graphique
plt.plot(abscisse, ordonnee, "ro") # en rouge
plt.show()
plt.close()
Résumé
👉 Pour pallier à ce problème, nous pouvons utiliser le deque du module collections
🌴 ma_liste.pop()
Recopier dans votre éditeur Python (pas sur Basthon) le script suivant, puis l'exécuter :
import timeit
import matplotlib.pyplot as plt
def suppression_fin(lst):
lst.pop()
# différentes tailles de listes notées n dans la suite
abscisse = [(10**7)*i for i in range(1, 11)]
print(abscisse)
ordonnee = []
for n in abscisse:
temps = 0
for i in range(2):
ma_liste = [0]*n # Création de liste de tailles n ne contenant que des 0
# Le chronométrage étant fait 2 fois, Il faut donc pour chaque mesure reprendre la liste initiale
temps += timeit.timeit("suppression_fin(ma_liste)", number=1, globals=globals())
ordonnee.append(temps)
# Graphique
plt.plot(abscisse, ordonnee, "go") # en vert
plt.show()
plt.close()
Résumé
Nous observons que ma_liste.pop() est beaucoup plus rapide que ma_list.pop(0). En effet, pour supprimer le premier élément d'une liste,
il faut tous les décaler d'un rang vers la gauche, alors que pour supprimer le dernier élément d'une liste, il suffit ... de supprimer
le dernier élément de la liste 😅.
Voici les résultats obtenus par les deux méthodes pour 100 mesures (il faut plus de 10 minutes pour créer cette image)
- Les listes ont des tailles allant de
- Les résultats sont exprimés en secondes

VIII. Crédits⚓︎
Romain Janvier, Gilles Lassus, Hugues Malherbe, Nicolas Revéret, Jean-Louis Thirot.
# Tests(insensible à la casse)(Ctrl+I)
(Alt+: ; Ctrl pour inverser les colonnes)
(Esc)