1 graphes generalites

Ce cours est très largement inspiré du cours de Gilles Lassus, qui s'est lui même intégralement inspiré du cours de Cédric Gouygou

I. Notion de graphe et vocabulaire

Le concept de graphe permet de résoudre de nombreux problèmes en mathématiques comme en informatique. C'est un outil de représentation très courant, et nous l'avons déjà rencontré à plusieurs reprises, en particulier lors de l'étude de réseaux.

1.1 Exemples de situations

1.1.1 Réseau informatique

1.1.2 Réseau de transport

1.1.3 Réseau social

1.1.4 Poster du courrier

Vous êtes le facteur d'un petit village, vous distribuez le courrier à vélo, à la seule force de vos jambes. Vous devez passer devant toutes les maisons du village, ce qui implique de traverser toutes les rues. Mais soucieux de préserver vos forces et de renouveler continuellement votre découverte des paysages, vous ne voulez pas traverser deux fois la même rue. Ici chaque nœud est un carrefour, et chaque arête une rue. Vous êtes en train de chercher un circuit Eulérien !

Il doit son nom à Leonhard Euler, qui chercha à savoir s'il était possible de franchir les 7 ponts de Königsberg sans jamais repasser deux fois sur le même (et en ne traversant le fleuve que grâce aux ponts, bien entendu).

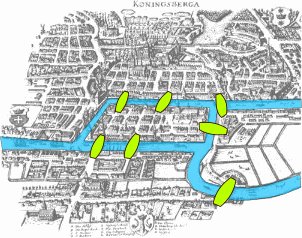
Source de l'image : http://zestedesavoir.com

1.1.5 Généralisation

Une multitude de problèmes concrets d'origines très diverses peuvent donner lieu à des modélisations par des graphes : c'est donc une structure essentielle en sciences, qui requiert un formalisme mathématique particulier que nous allons découvrir.

L'étude de la théorie des graphes est un champ très vaste des mathématiques : nous allons surtout nous intéresser à l'implémentation en Python d'un graphe et à différents problèmes algorithmiques qui se posent dans les graphes.

1.2 Vocabulaire

En général, un graphe est un ensemble d'objets, appelés sommets ou parfois nœuds (vertex or nodes en anglais) reliés par des arêtes ou arcs ((edges en anglais)). Ce graphe peut être non-orienté ou orienté .

1.2.1 Graphe non-orienté

Dans un graphe non-orienté, les arêtes peuvent être empruntées dans les deux sens, et une chaîne est une suite de sommets reliés par des arêtes, comme C - B - A - E par exemple. La longueur de cette chaîne est alors 3, soit le nombre d'arêtes.

Les sommets B et E sont adjacents au sommet A, ce sont les voisins de A.

Exemple de graphe non-orienté : le graphe des relations d'un individu sur Facebook est non-orienté, car si on est «ami» avec quelqu'un la réciproque est vraie.

1.2.2 Graphe orienté

Dans un graphe orienté, les arcs ne peuvent être empruntés que dans le sens de la flèche, et un chemin est une suite de sommets reliés par des arcs, comme B → C → D → E par exemple.

Les sommets C et D sont adjacents au sommet B (mais pas A !), ce sont les voisins de B.

Exemple de graphe orienté : le graphe des relations d'un individu sur Twitter est orienté, car on peut «suivre» quelqu'un sans que cela soit réciproque.

1.2.3 Graphe pondéré

Un graphe est pondéré (ou valué) si on attribue à chaque arête une valeur numérique (la plupart du temps positive), qu'on appelle mesure, poids, coût ou valuation.

Par exemple:

• dans le protocole OSPF, on pondère les liaisons entre routeurs par le coût;
• dans un réseau routier entre plusieurs villes, on pondère par les distances.

1.2.4 Connexité

Un graphe est connexe s'il est d'un seul tenant: c'est-à-dire si n'importe quelle paire de sommets peut toujours être reliée par une chaîne. Autrement un graphe est connexe s'il est «en un seul morceau».

Par exemple, le graphe précédent est connexe. Mais le suivant ne l'est pas: il n'existe pas de chaîne entre les sommets A et F par exemple.

Il possède cependant deux composantes connexes : le sous-graphe composé des sommets A, B, C, D et E d'une part et le sous-graphe composé des sommets F, G et H.

II. Modélisations d'un graphe

Pour modéliser un graphe, il faut établir par convention une manière de donner les renseignements suivants :

• qui sont les sommets ?
• pour chaque sommet, quels sont ses voisins ? (et éventuellement quel poids porte l'arête qui les relie)

2.1 Représentation par matrice d'adjacence

Principe

• On classe les sommets (en les numérotant, ou par ordre alphabétique).
• on représente les arêtes (ou les arcs) dans une matrice, c'est-à-dire un tableau à deux dimensions où on inscrit un 1 en ligne i et colonne j si les sommets de rang i et de rang j sont voisins (dits aussi adjacents).

Ce tableau s'appelle une matrice d'adjacence (on aurait très bien pu l'appeler aussi matrice de voisinage).

2.1.1 Graphe non orienté

Dans ce graphe non orienté, comme B est voisin de C, C est aussi voisin de B, ce qui signifie que l'arête qui relie B et C va donner lieu à deux "1" dans la matrice, situé de part et d'autre de la diagonale descendante (un mathématicien parlera de matrice symétrique).

2.1.2 Graphe orienté

2.1.3 Graphe pondéré

Exercice 1

Soit un ensemble d'amis connectés sur un réseau social quelconque. Voici les interactions qu'on a recensées:

• André est ami avec Béa, Charles, Estelle et Fabrice,
• Béa est amie avec André, Charles, Denise et Héloïse,
• Charles est ami avec André, Béa, Denise, Estelle, Fabrice et Gilbert,
• Denise est amie avec Béa, Charles et Estelle,
• Estelle est amie avec André, Charles et Denise,
• Fabrice est ami avec André, Charles et Gilbert,
• Gilbert est ami avec Charles et Fabrice,
• Héloïse est amie avec Béa.

Q1. Représenter le graphe des relations dans ce réseau social (on désignera chaque individu par l'initiale de son prénom). Il est possible de faire en sorte que les arêtes ne se croisent pas !

Solution Q1

Q2. Donner la matrice d'adjacence de ce graphe.

Solution Q2

\(\pmatrix{ 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ }\)

Exercice 2

Construire les graphes correspondants aux matrices d'adjacence suivantes:

Q1. \(M_1 =\pmatrix{ 0&1&1&1&1\\ 1&0&1&0&0\\ 1&1&0&1&0\\ 1&0&1&0&1\\ 1&0&0&1&0\\ }\)

Solution Q1

Q2. \(M_2=\pmatrix{ 0&1&1&0&1\\ 0&0&1&0&0\\ 0&0&0&1&0\\ 1&0&0&0&1\\ 0&0&0&0&0\\ }\)

Solution Q2

Q3. \(M_3=\pmatrix{ 0&5&10&50&12\\ 5&0&10&0&0\\ 10&10&0&8&0\\ 50&0&8&0&100\\ 12&0&0&100&0\\ }\)

Solution Q3

2.1.5 Implémentation Python des matrices d'adjacence

Matrices d'adjacence en Python

Une matrice se représente naturellement par une liste de listes.

Exemple: La matrice \(M_1 =\pmatrix{ 0&1&1&1&1\\ 1&0&1&0&0\\ 1&1&0&1&0\\ 1&0&1&0&1\\ 1&0&0&1&0\\ }\), associée au graphe suivant

sera représentée par la variable G suivante :

G = [[0, 1, 1, 1, 1],
      [1, 0, 1, 0, 0],
      [1, 1, 0, 1, 0],
      [1, 0, 1, 0, 1],
      [1, 0, 0, 1, 0]]

Complexité en mémoire et temps d'accès :

• Pour un graphe à \(n\) sommets, la complexité en mémoire (appelée aussi complexité spatiale) de la représentation matricielle est en \(O(n^2)\).

• Tester si un sommet est isolé (ou connaître ses voisins) est en \(O(n)\) puisqu'il faut parcourir une ligne, mais tester si deux sommets sont adjacents (voisins) est en \(O(1)\), c'est un simple accès au tableau.

La modélisation d'un graphe par sa matrice d'adjacence est loin d'être la seule manière de représenter un graphe : nous allons voir une autre modélisation, par liste d'adjacence.

2.2 Représentation par listes d'adjacence

listes d'adjacence ... avec un dictionnaire

• On associe à chaque sommet sa liste des voisins (c'est-à-dire les sommets adjacents). On utilise pour cela un dictionnaire dont les clés sont les sommets et les valeurs les listes des voisins.

• Dans le cas d'un graphe orienté on associe à chaque sommet la liste des successeurs (ou bien des prédécesseurs, au choix).

Par exemple, le graphe

sera représenté par le dictionnaire :

G = {'A': ['B', 'C', 'D', 'E'],
     'B': ['A', 'C'],
     'C': ['A', 'B', 'D'],
     'D': ['A', 'C', 'E'],
     'E': ['A', 'D']
    }

listes d'adjacences ... avec une liste

Dans le cas où les sommets sont numérotés de \(1\) à \(n-1\) pour un graphe de taille \(n\), le dictionnaire précédent peut être remplacé par une liste de listes liste_adjacence:

• liste_adjacence[0] contient la liste des voisins du sommet 0
• liste_adjacence[i] contient la liste des voisins du sommet i

Ce graphe a pour liste d'adjacence implémentée avec un dictionnaire :

{
    0: [1, 2, 3],
    1: [2],
    2: [0],
    3: [2]
}

Ce graphe a pour liste d'adjacence implémentée avec une liste :

[
    [1, 2, 3],
    [2],
    [0],
    [2]
]

Complexité en mémoire et temps d'accès :

• Pour un graphe à \(n\) sommets et \(m\) arêtes, la complexité spatiale de la représentation en liste d'adjacence est en \(O(n+m)\). C'est beaucoup mieux qu'une matrice d'adjacence lorsque le graphe comporte peu d'arêtes (i.e. beaucoup de 0 dans la matrice, non stockés avec des listes).

• Tester si un sommet est isolé (ou connaître ses voisins) est en \(O(1)\) puisqu'on y accède immédiatement, mais tester si deux sommets sont adjacents (voisins) est en \(O(n)\) car il faut parcourir la liste.

2.2.1 Exercices

Exercice 3

Construire les graphes correspondants aux listes d'adjacence suivantes.

Q1.

G1 = {
'A': ['B', 'C'],
'B': ['A', 'C', 'E', 'F'],
'C': ['A', 'B', 'D'],
'D': ['C', 'E'],
'E': ['B', 'D', 'F'],
'F': ['B', 'E']
     }

Solution Q1

Q2.

G2 = {
'A': ['B'],
'B': ['C', 'E'],
'C': ['B', 'D'],
'D': [],
'E': ['A']
     }

Solution Q2

Exercice 4

Construire le graphe correspondant à la liste d'adjacences suivante.

[
    [1, 2, 3],
    [0, 4, 5],
    [],
    [2],
    [5],
    [2, 4],
]

Solution

III. Visualiser un graphe

1. Avec le module netwoks

Exemple de graphe

On donne le graphe suivant à l'aide du dictionnaire donnant pour chaque sommet la liste des voisins (ou successeurs)
dico = {0:[1, 2], 1:[0, 2, 3], 2 : [0, 1, 3], 3: [1, 2]}

Ce graphe est-il orienté? Pourquoi? Représentez ce graphe sur votre cahier.

Solution

Ce graphe n'est pas orienté, car les arcs entre deux sommets existent tous dans les deux sens.
⏳ Pour sa représentation, voir ci-dessous.

La bibliothèque netwoks

Pour visualiser ce graphe, nous allons utiliser les bibliotèques netwoks et matplotlib.
⏳ Attention, ce n'est pas instantané. Quand vous exécuterez une cellule, une étoile s'affichera dans la barre latérale, signifiant que basthon "travaille" ... Attendre qu'elle disparaisse avant d'exécuter la cellule suivante.

A vous de jouer : testez vos propres graphes ci-dessous

2. Avec le module graphviz

Astuce pour exécuter une cellule dans un notebook

Raccourci clavier : Nous allons utiliser la touche Maj + Entrée

Graphe orienté

Graphe non orienté

IV. Création d'une classe Graphe

Dans cette partie, nous ne traiterons que des graphes non-orientés.

Interface souhaitée

Nous voulons que le graphe puisse être créé grâce aux instructions suivantes :

Python

g = Graphe(['A', 'B', 'C', 'D', 'E'])
g.ajouter_arete('A', 'B')
g.ajouter_arete('A', 'C')
g.ajouter_arete('A', 'D')
g.ajouter_arete('A', 'E')
g.ajouter_arete('B', 'C')
g.ajouter_arete('C', 'D')
g.ajouter_arete('D', 'E')

Une classe Graphe

Python

class Graphe:

def __init__ (self, sommets):
    self.sommets = sommets
    self.dic = {sommet: [] for sommet in self.sommets} # création par compréhension

def ajouter_arete(self, x, y):
    if y not in self.dic[x]:
        self.dic[x].append(y)
    if x not in self.dic[y]:
        self.dic[y].append(x)

def get_sommets(self):
    return self.sommets

def get_voisins(self, x):
    return self.dic[x]

def get_dictionnaire(self):
    return self.dic

A quoi voit-on que le graphe créé est non orienté ?

Solution

La fonction ajouter_arete(self, x, y) ajoute, s'il n'y est pas déjà, y dans la liste d'adjacence de x, et x dans la liste d'adjacence de y.

Une classe Graphe

Utiliser la classe Graphe ci-dessous pour créer le graphe dont on donne le dictionnaire des listes d'adjacences:
dico = {0:[1, 2], 1:[0, 2, 3], 2: [0, 1, 3], 3: [1, 2]}

Pour vérifier, vous ferez afficher le dictionnaire obtenu, puis le graphe. Vous pourrez pour cela procéder de façon analogue à ce que l'on a déjà vu.

Solution

Python

g2 = Graphe([0, 1, 2, 3])
g2.ajouter_arete(0, 1)
g2.ajouter_arete(0, 2)
g2.ajouter_arete(1, 2)
g2.ajouter_arete(1, 3)
g2.ajouter_arete(2, 3)

Puis pour la représentation :

Python

dict_2 = g2.get_dictionnaire()
print(dict_2)
plt.cla()
G2 = cree_graphe_non_oriente_nx(dict_2)
nx.draw_circular(G2, with_labels = True)
plt.show()